◆ Solving Unsteady Separated Flow Using Large Eddy Simulation in ADINA
CFD
ADINA
CFDのLarge Eddy Simulationによる非定常剥離流れの解析
CFDにおいて最も重要なことは、十分に正確かつ効率的な乱流モデリ
ングです。Large Eddy Simulation (LES)
はとても正確であると考えられていますが、一方で計算のコストがとても高いことが知られています。よって現在のところ、LESが複雑な工業的形状に適応さ
れることはほとんどありません。(下記のリファレンス、2000年のSpalartの例を見てください。)
しかし、コンピューター性能が上がり、またアルゴリズムがより効率的になったため、LESは広範囲で使われるようになるでしょう。ADINAでの解析結果を説
明するため、私たちは、2006年7/30のニュース紹介した、壁に
かかった立方体の障害物を通り過ぎる流れの問題を再度取り上げます。障害物は単純で
すが、例えば飛行機や自動車産業で出会うようなより複雑な形状でも可能です。発表されている実験データとの比較のために単純な障害物を用いています。
ここで紹介しているのはSmagorinsky-Lillyサブグリッドスケールモデルを用いて得られたLESの結果です。流入口における完全に発達した
速度プロファイルとランダム摂動は重ねあわされています。全1500タイムステップが使われました。平均流れ量を計算するためのサンプリングは、最後の
250ステップからとりました。空間と時間の離散化は、両方とも2次精度です。メッシュは比較的粗く約650,000 3D要素です。
上のムービーは、ブロックの対称面における、無秩序のような時間依存の流れ方向速度のコンター図です。ムービーと同じ面における時間平均の流れ方向速度の
コンターは下に示しています。また、ブロック底部から0.05hの位置の水平面における時間平均の結果も示しています。ここでhはブロックの高さです。
アニメーションと時間平均結果から流れのおもな特徴が見られます。つまり、上流の剥離域、二箇所の下流の剥離域、ブロック上部の再循環域です。下流の一つ
目の剥離域において、瞬間的な流れは、時間平均流れと大きく異なって見えることに注意してください。
以下の表で示すのは、ADINAでの剥離領域の長さと、論文で得られたいくつかのもっとも正確なベンチマーク(LESを使った実験的、数値的結果)の結果
の比較です。3つ全ての再循環領域の長さで素晴らしい一致が見られます。
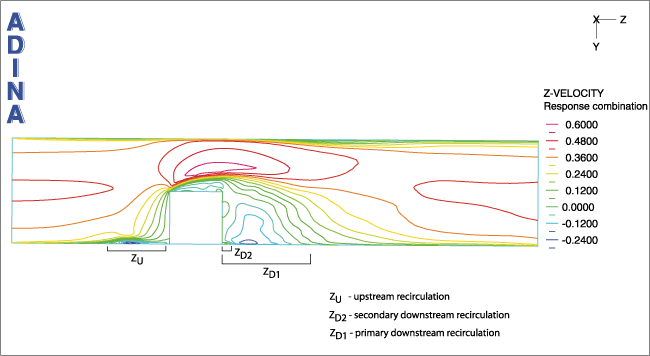
対称面における時間平均の流れ方向速度のプロット
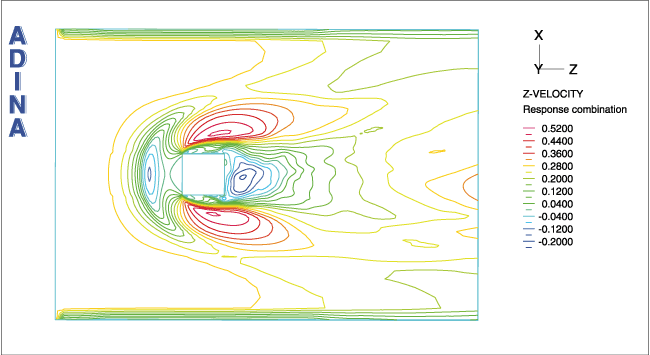
ブロックの底から高さ0.05hにおける時間平均の流れ方向速度のプ
ロット
| |
ADINA CFD
(LES) |
Martinuzzi
&
Tropea, 1993
(Experiments) |
Shah, 1998
(LES)
>106 cells |
Rodi et al., 1997
(LES) |
| 上流の再循環 |
1.140 |
1.040 |
1.080 |
0.998 |
下流の一つ目の再循環
|
1.670 |
1.612 |
1.690 |
1.432 |
下流の二つ目の再循環
|
0.166 |
- |
0.160 |
0.134 |
(再
循環領域の長さは、ブロックサイドの長さhによって正規化しました)
References
Spalart P. R., Strategies
for turbulence modeling and simulations, International Journal of
Heat and Fluid Flow, 21 (2000), 252-263.
Shah K.B., Large eddy
simulation of the flow past a cubic obstacle, Ph. D. Thesis (1998)
Martinuzzi R., and Tropea,
C., The flow around surface mounted prismatic obstacles placed in a
fully developed channel flow, ASME Journal of Fluids Engineering,
115 (1993) 85-93.
Rodi W., Comparison of LES
and RANS calculations of the flow around bluff bodies, Journal of
Wind Engineering and Industrial Aerodynamics, 69-71 (1997)
55-75.
|

