ADINAによる3次元破壊力学
2012.2.15 3D Fracture Mechanics with ADINA

ADINAによる3次元破壊力学
亀裂のふるまい方を含む破壊機構の有限要素解析は最も重要なことであるにちがいない。 特に、電力施設や航空機には亀裂とそれが進展するかどうか継続して検査する必要がある。 まず最初は、線形弾性破壊力学解析をJ積分を計算して実行する。
ADINAはこのような解析に有効に使える。ここでは、ADINAによる3次元亀裂のJ積分の計算 のための代表的な解析手順を特集する。
3次元破壊力学の計算には、亀裂前縁周辺にかなり細かい特別なメッシュを使うのが普通である。 ADINAユーザーインターフェース(AUI)はこのようなメッシュを生成するための特別な機能がある。 この機能はADINA-Mの形状モデラーにあり、パラソリッドでもオープンカスケードでもどちらでも 使える。
この機能を実演するために、3次元解析における代表的な面亀裂のモデリングを取り上げる。 亀裂の両側に形状があるので、対称性は利用しない。図1にこの典型的な亀裂の図を示す。
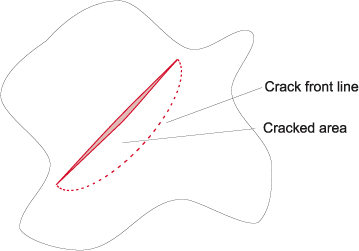
図1 取り上げた典型的な亀裂の図
形状モデリング
亀裂のない形状を通常のADINA-Mモデリング機能を使って作成する。
亀裂前縁をエッジで表現する。このエッジは亀裂方向に向けられたローカル座標系を用いて 簡単に定義できる。
図2で表すように、亀裂前縁に直接に隣接している形状は、亀裂の両側に一つずつのボディとして、 二つのボディーで作成する。これらのボディーは亀裂前縁ボディーと呼ぶことにする。それらは、 亀裂前縁に対応する各ボディーの一つのエッジと亀裂前縁近傍の亀裂断面に対応する各ボディーの 一つのフェースを持つ半分の円柱形状である。
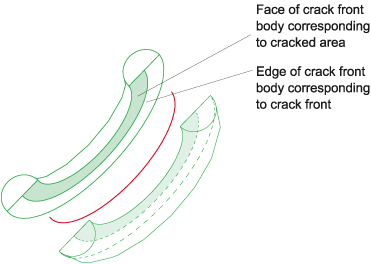
図2 亀裂前縁ボディー(亀裂部を分解した図)
亀裂前縁ボディー周辺の形状は、図3に示すように亀裂の両側に一つづつのボディで、 二つのボディーで作成する。これらのボディーは亀裂被覆ボディーと呼ぶことにする。 亀裂被覆ボディーは亀裂前縁ボディーは含まないで亀裂断面を含む十分に大きな領域 にしなければならない。このように定義する亀裂は亀裂前縁ボディーと亀裂被覆ボディー で囲まれている。
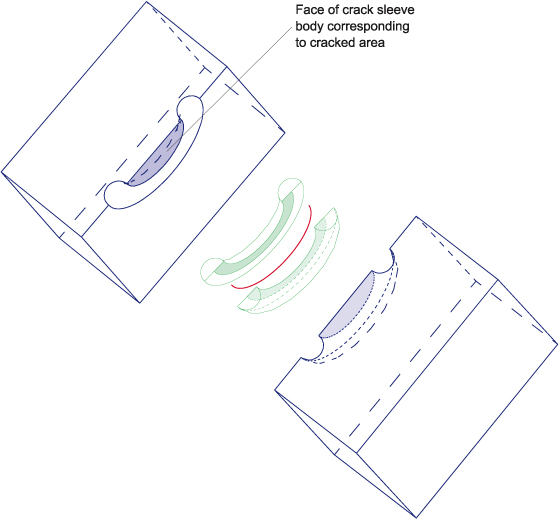
図3.亀裂被覆ボディーと亀裂前縁ボディー(分解図)
モデルに亀裂を作るために、亀裂前縁ボディーと亀裂被覆ボディーは亀裂なしのボディー から論理差を取る。全てのボディー間で一致したメッシュを作成するのにフェースリンク を用いる。
メッシング
マップドメッシュコマンドによって亀裂前縁ボディーにメッシュを作成する。このコマンドは 亀裂先端ライン近傍でウェッジ要素でマップされたメッシュを生成する。要素は、ウェッジ要素 が扇状に配置される。このコマンドでは亀裂断面に対応するフェース上で自動のnodal coincidence checkingを使わない。さらには、高次要素の中間節点を1/4位置に移動させる ためのオプションもある。(このオプションは亀裂前縁ライン近傍のウェッジ要素ののみに 適用する。)このマップドメッシュを図4に示す。
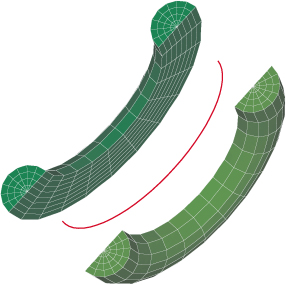
図4 亀裂前縁ボディーに用いたマップドメッシュ(分解図)
亀裂被覆ボディーはフリーフォームメッシュコマンドを用いてメッシュ作成する。図5に示す。 このフリーフォームメッシングコマンドでは亀裂断面に対応するフェース上で自動の nodal coincident checkingを使わない。
残りのボディーは通常のフリーフォームメッシングでメッシュ作成する。

図5 ボディーごとのメッシュ(分解図)
仮想移動
破壊力学計算で必要となる仮想移動は以下の表によって自動的に作成される。
| Virtual shift number | Corner node number on crack front | Ring number |
| 1 | 1st corner node | 0 |
| 2 | 2nd corner node | 0 |
| ... | ||
| N | Nth corner node | 0 |
| N + 1 | 1st corner node | 1 |
| ... | ||
| 2 x N | Nth corner node | 1 |
| ... | ||
| nring x N | Nth corner node | nring - 1 |
ここで、Nは亀裂前縁上のコーナー節点の数、nringは亀裂前縁周囲のマップドメッシュの円管の数である。
Ring0は亀裂前縁のコーナー節点のみの移動を表している。Ring1は、同節点とその節点周りの 一番目の円管の要素の移動である。このプロセスをより大きなring数で繰り返す。
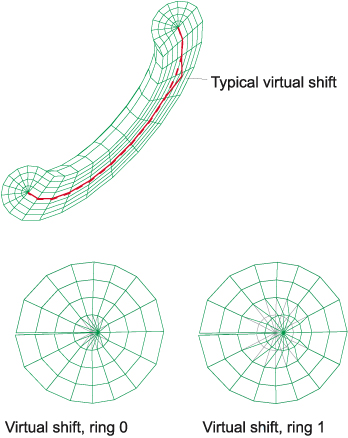
図6 仮想移動の図
J積分の経路の独立性によって、仮想移動j、j+N、J+2×N、...におけるJ積分値 は同じになる。この、経路の独立性を仮想移動を用いて検証することができた。
例
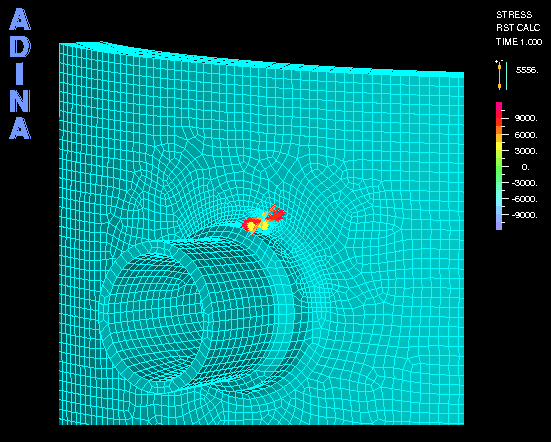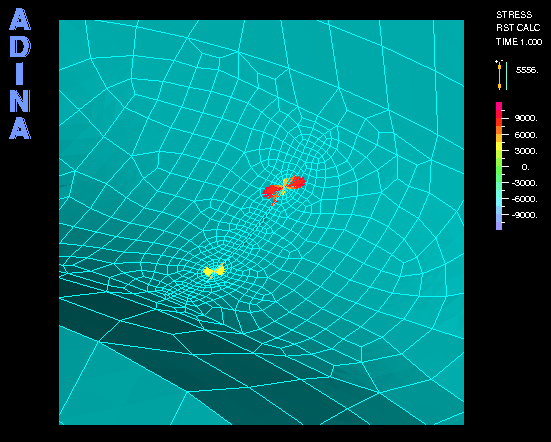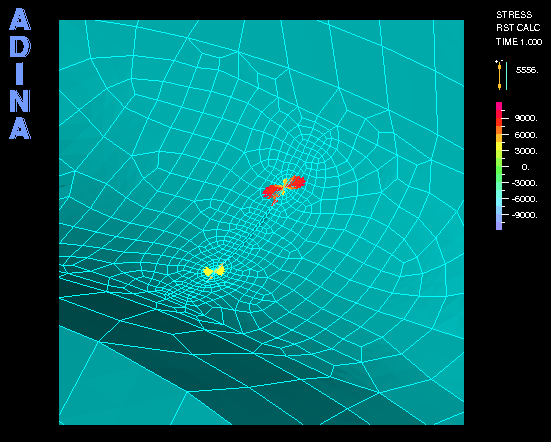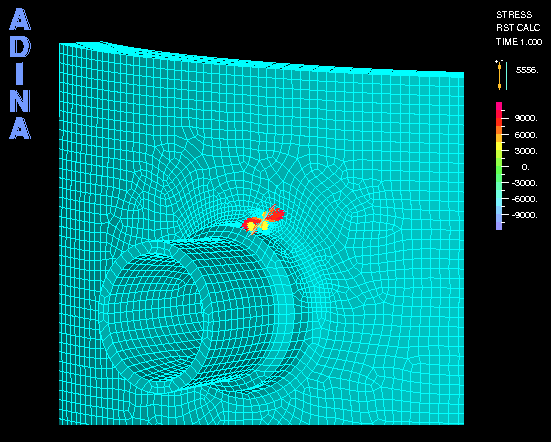
上の動画は、メッシュモデルと圧力容器に亀裂面が存在する場合に内部圧力による応力である。
J積分の結果を図7に示す。
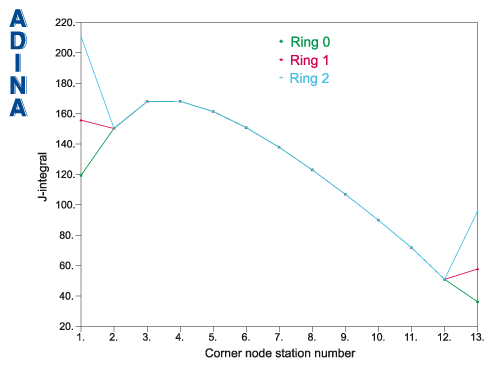
図7 ring0,1,2におけるJ積分値のプロット仮想移動の図
亀裂前縁のはじめと最後のコーナー節点では、ring1,2...の仮想移動が モデルの境界上での仮想移動になっているので適切ではない。モデルの境界は 曲がっており、亀裂前縁は境界に垂直ではない。つまり、このような仮想移動 は形状の境界を乱すことになる。
亀裂前縁上のその他のコーナー節点では、思いどうりにJ積分の経路の独立性が 見てわかる。
ADINAユーザーインターフェースのモデリング機能とADINAの計算は破壊力学計算 で非常に有用であることがわかる。
Keywords:破壊力学、亀裂前縁、J積分、仮想移動、有限要素、亀裂モデリング
