Physical Instabilities in FSI

流体-構造の相互作用における問題には物理的な不安定を示すことがよく

知られています。したがって、このような不安定を正確に求めることができる

数値計算技術のみを使ってシステムのふるまいを検証することが重要になります。

さらに重要なことは、実際の物理現象を妨げるような数値安定性を計算手法に

導入すべきではありません。

短的に二つの例を紹介します。最初の例は、底部が柔軟体の上部移動流れにおける

流体構造相互作用です。2つめの例は、物理的な不安定現象、例えばフラッターの

ような問題の流体構造相互作用でどのようにADINA FSIを利用することができるかを

示します。

図1は、最初の例の概略図を示しています。くぼ地の上部は開放されていて垂直の

剛壁と底部を柔らかい板で囲まれていて、この開放された上面に周期的な水平速度

が与えられています。(図参照)　モデルの詳細は図に示されています。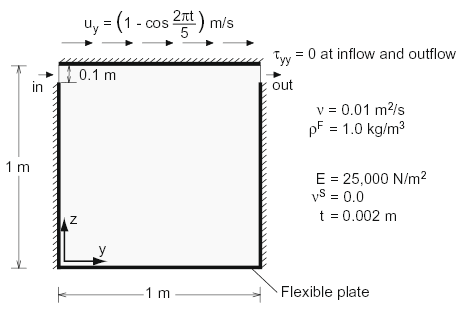

図1：くぼ地のせん断流れ問題の図

時間変化の応答を計算するのですが、問題では、最大流速が与えられいてるときの

定常応答を最初に計算します。(図1）　この部分の検証の目的は、ADINA CFDの

アダプティブメッシュの機能を用いて良好なメッシュを求めるためでした。

適切になったメッシュを非定常計算に利用します。

さらに、システムの応答は120×120の均一な分割の4節点　FCBI要素を用いて

解析します。適切になったメッシュと均一な解像度の4節点要素メッシュを用いて

非定常解析の結果は図2と図3に比較してあります。

二つの解析には、底部の柔軟な板は2節点のアイソパラメトリック平面ひずみビーム要素

を用いてモデル化しました。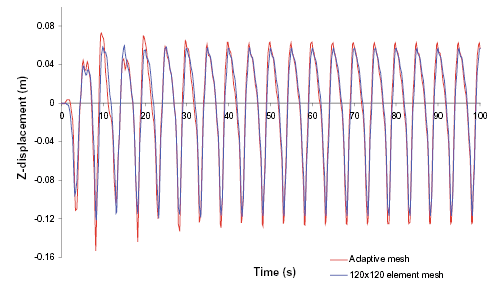 

図2：柔軟な板の中間点における垂直方向変位の時間履歴

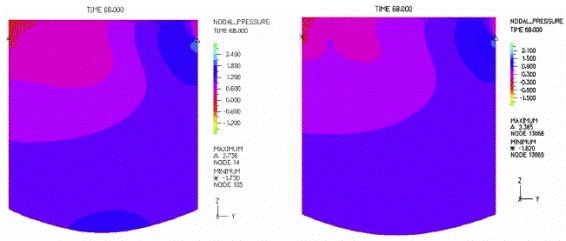
(a) 適切になったメッシュの結果　　　　　　(b) 均一メッシュの結果

図3：適切になったメッシュと均一メッシュを用いた時刻68の圧力

下の最初の動画は適切になったメッシュを用いて解かれたときの粒子軌跡を表して

います。その次の動画は、同メッシュを用いての流れの流速ベクトを示しています。

計算の中で底部が柔軟に上下動しているのが興味深いところです、平均変位を下に

示してあります。(図2)

図1で与えられたパラメーターでは、上の問題は物理的な不安定は現れず、

長時間の計算の後でもなお図2のようにそれがわかります。計算では、如何なる

不安定も確認されません。。

2番目の例は、翼のフラッター問題です。用いた3DのCFDメッシュと翼を拡大した

ものを図4に示してあります。流入速度は、12m/sです。流出口は開放されたのみで

その他の流体境界は壁の条件をモデル化しています。

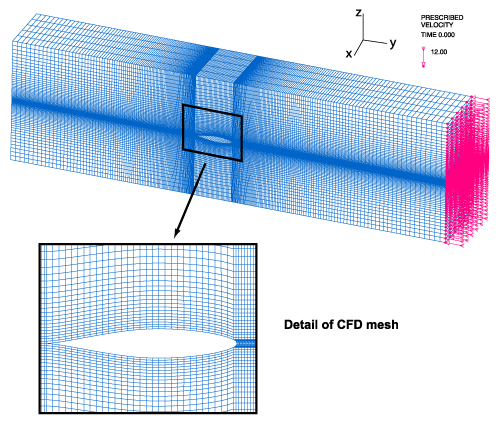
 図4：フラッタ問題のCFDメッシュ

流体はk-ω乱流モデルを用いた非圧縮性ナビエ-ストークス流体とし、FCBI-C要素

を用いて離散化します。翼は、4節点シェル要素を用います。単純に翼の一部分だけ

を考え、柔軟性と翼の質量は横方向とねじれ方向のばねおよび集中質量を使って

モデル化しています。わずかな変動荷重を翼のZ方向に与えています。

ページ先頭の動画は、振動していることを表しており、図5では、翼のピッチング

とプランジングの時間履歴を表示しています。ご覧いただければ、翼の振動が

始まり、振動が時間の経過とともに大きくなっているのがわかります。

これがフラッター現象の本質的な特徴になります。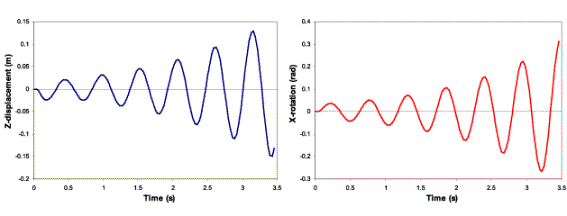

 図5：翼の変位と回転のグラフ

下の動画は、流体の速度の大きさと節点圧力のコンター表示です。

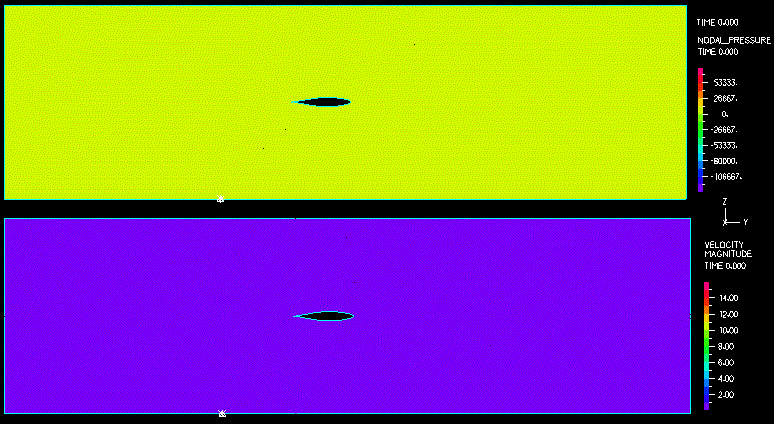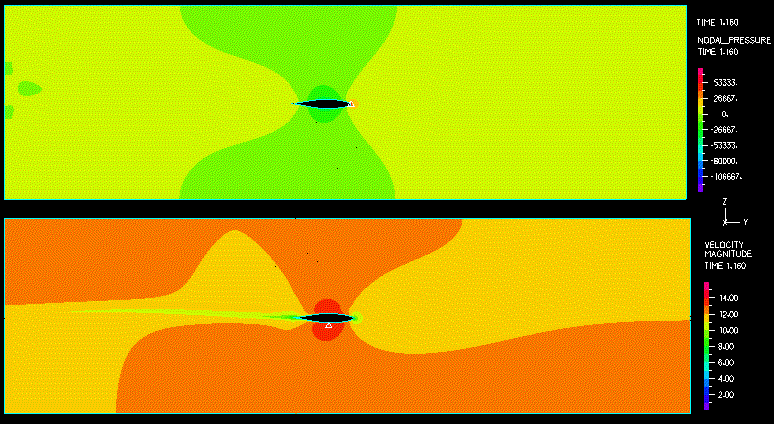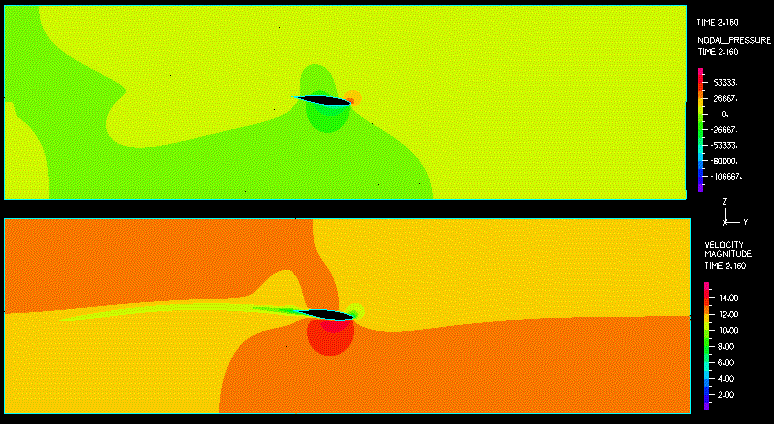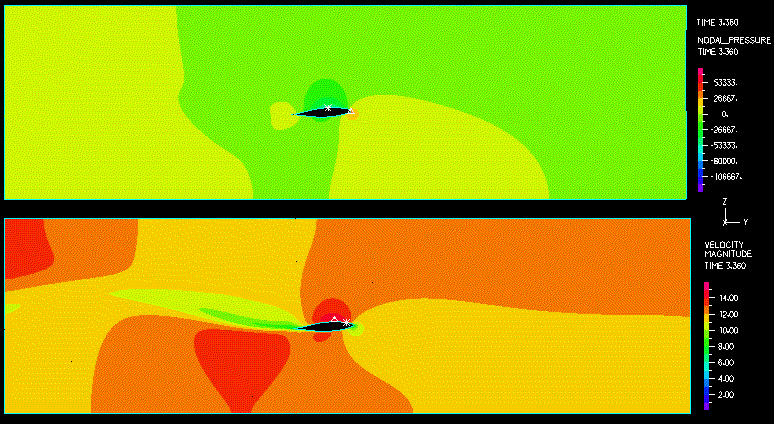
上の例は、FSIにおけるADINAの解析能力の一部を示したものです。様々な

検証例の概要や出版物は、ADINA-FSI　に与えられています。 

Keywords:

Fluid-structure interaction, FSI, transient analysis, FCBI, FCBI-C,

adaptive meshing, flutter, physical instability, aeroelasticity 

References

1.                        K.J. Bathe, H. Zhang, "A mesh adaptivity procedure for CFD and

 　     fluid-structure interactions", Computers and Structures,

   　   87:604-617, 2009.

2.　　　U. Küttler, W. Wall, "Fixed-point fluid-structure interaction solvers with dynamic relaxation",

　　　 Comput Mech, 43:61-72, 2008.