以前のニュースで、流体と構造の相互作用の有限要 素解析を紹介しましたが、その際には温度の効果は考慮されていませんでした。下のリファレンスもご覧ください。

解析に温度変化の条件を含まなければならない問題 は、もちろんたくさんあります。温度は、問題の領域上で空間的に変化するかもしれませんし、時間関数を持って変化するかもしれません。ここで考慮される問 題の領域は、固体/構造と流体が完全連成します。構造の変形や応力などの解析結果における温度変化の影響は非常に大きいことがあります。

ADINAはこのような問題（ニュースをご覧くだ さい）に、特に強力なツールです。シミュレーションには以下の条件を含むことができます。

要点を押さえたシンプルな２例題の解析でこれらの 機能の説明をします。ここでは完全連成の条件が使われています。

Problem1

下の図で示すのは、温度勾配と内部流体圧力を受け るゴムリングです。（Ogden材料モデル）リングの外半径は2から8.72まで膨らみました。これは大 変形を受けているのは明らかです。このシミュレーションでは、流体の領域は徐々に大きくなっていくため、流体メッシュは、ゴムリングの膨張とともに広がっ ていきます。上のムービーはリングと流体のレスポンスを示しています。

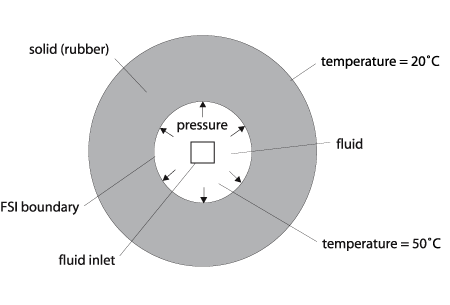
Problem1の概要

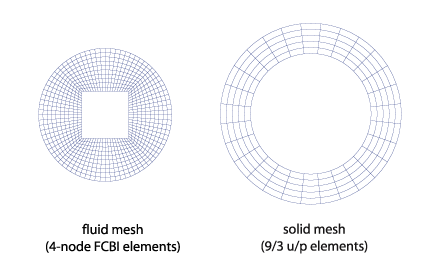
Problem1で使用したメッシュ

Problem 2

二つ目の問題で は、接線方向に流体の流れを受ける プレートを考えます。プレートの両端は固定されていて、流体の温度の上昇が熱座屈を引き起こします。プレートは熱塑性材料でモデル化され、温度依存の降伏 応力と線膨張係数を定義しています。以下に問題の概要、有限要素メッシュ、いくつか の結果を示します。

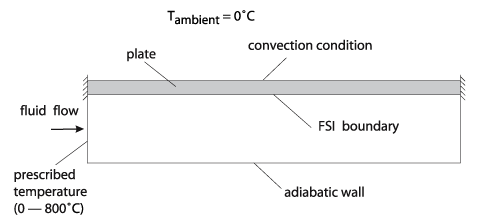
Problem2の概要

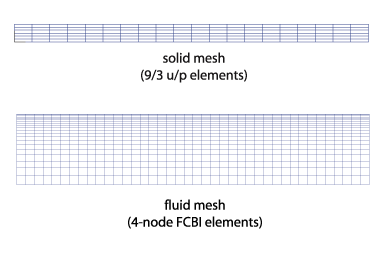
Problem2で使われたメッシュ

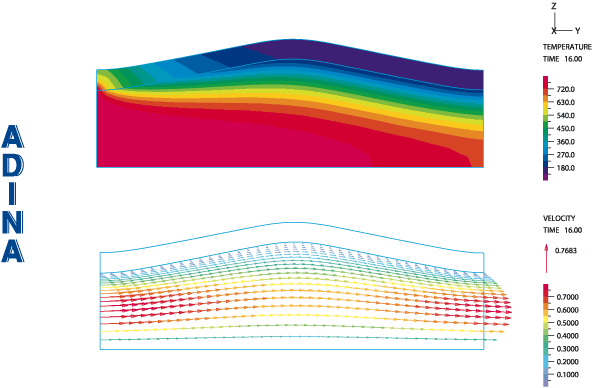
Problem 2の結果　：温度と速度のプロット

等方弾性材料、 一様な温度上昇、ごく小さな流体圧 力を仮定した結果は、ビーム理論に基づく解析解と比較できます。下の最後のグラフでは、与えられた温度に対する、プレートの中央における垂直方向の変位 （プレートの長さによって正規化されています）で比較しています。座屈荷重と座屈後の変位は解析結果と一致しています。

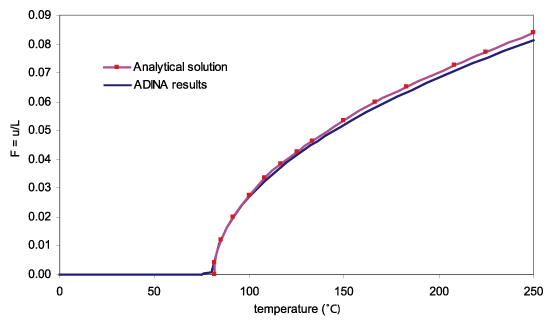
単純なProblem2の結果と解析解の比較

ADINAで温 度効果を含む FSI解析を行うことは、様々な産業で生じる多くの問題のシミュレーションに非常に有用です。

Reference

K. J. Bathe and G.A. Ledezma, Benchmark problems for incompressible fluid flows with structural interactions, Computers & Structures, 85, 628-644, 2007.