|
Bathe法-物理減衰無し
Newmark法-物理減衰無し
Accurate Implicit Time Integration in Nonlinear
Dynamic Analysis
正確な非線形動解析での陰的時間積分
動的問題の有限要素法の離散化から求められる、常微分方程式の正確な計算は、過去20〜30年間で、
広範囲の研究がされてきました。
安定性と動解析の正確さの問題点は、線形問題において詳細に述べられています。(参考文献[1])
しかしながら、いくつかの分野の非線形動的問題に関しては、議論の余地があります。
このニュースでは、私達はそんな1問題を考え、正確な評価ができる、異なる時間進行法(Bathe
法やNewmark法)の結果において、これらの適合性を比較します。
台形則が非線形の動解析問題に適用される時、特に、大変形で長い時間の動的問題に対 して不安定になりえることが立証されています。(参考文献[2]) この研究では、私達はもう1つの重要な問題である、接触により起こる不安定問題の分野も考えます。 接触での結果はがたつき、そのうえ、FSI解析での構造と流体間のカップリングの影響もします。 研究を行うためにテスト用の有限要素解析を用意しました、そしていくつかの本質がわ かってきました。(図1参照) モデルは、全体が弾性のシェル要素で作成されていて、底面が完全拘束されています。 そして、剛体の外壁をふまえた流体が覆っています。 媒体を表現するのに、MITC4シェル要素と、亜音速のポテンシャル流体要素が使われてます。 シェル構造体は、摩擦接触状態の2部品で構成されてます。 モデルは、流体流動より突然起こるパイプ破損を表します。 衝撃の結果は、モデルの内部部品が急激に変化し接触する原因となります。 そのような問題での陰的動解析では、通常Newmark時間積分法が使われます。 しかしながら、接触状態が、内部部品を含む時、接触面は、滑らない状態(STICK)と滑る状態(SLIP)を 繰り返し、結果が流体内が急速加圧されます。 構造によるカップリングにより、壁の高周波の振動がまた起こります。 これらの高周波振動は、Newmark法での解析では、不要波です。 そして、時間と共に成長し、解析上で明らかに大きな不要波になります。 減衰無しでNewmark法を使った結果を図2に示します。 フランジの高振動応答に注目します。内部部品間は、不連続な接触状態です。 また、寄生した圧力は構造と流体の両方の物体間を拡散します。 この問題を解決するためには、いくつか方法があります。: ・物理的な減衰をモデルに追加(例:レイリー減衰)。このケースでは、減衰は構造のみ に適用されます。 課題は、物理的に無視できるとき、どれくらいの大きさの減衰を与えるかです。 ・数値減衰の追加。これは、数値振動を減少し、しかし、解析すべき物理応答もまた減少します。 そして、課題は許容できる結果を得るのに、どれ位の数値減衰を入力するかです。 ・ADINAで利用可能なBathe時間積分法を使用する手法です。この手法は時間ステップ毎に2つのサブ ステップにする手法に基づいています。 最初のサブステップで、一般台形則を使い、次のサブステップで、後退差分法を使います。 手法は、2次精度近似です。そして、小さい数値減衰が用いられます。 (調整パラメータは有りません。そして、時間ステップのサイズ依存するだけです。) 効率的に高周波モードを減衰します。(参考文献[2]) 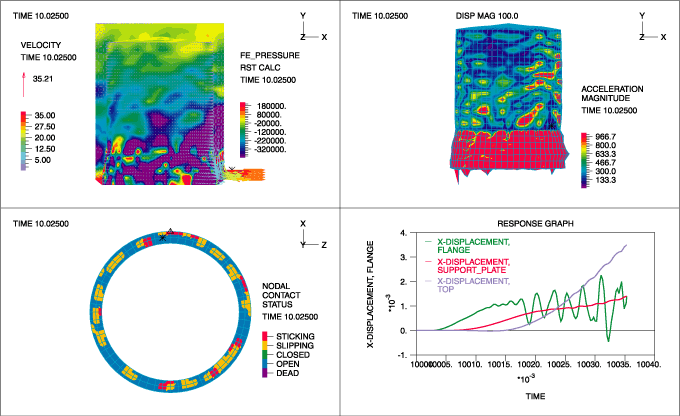
図1 問題の概略図 図3〜5 は上記で述べられている、異なる時間積分技術で使ったシステムの応答を示してます。 時間ステップサイズは常に同じです。 
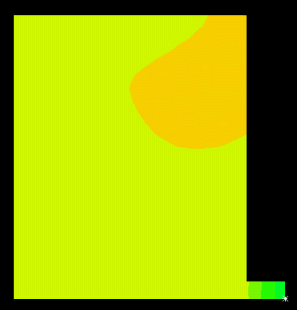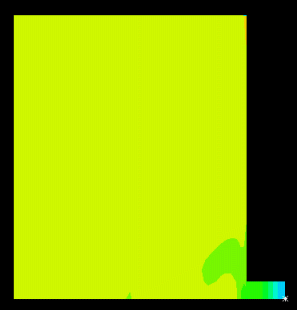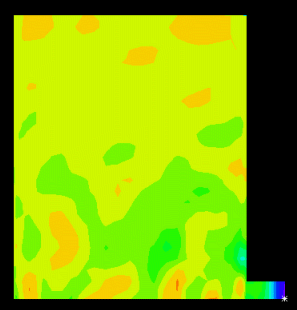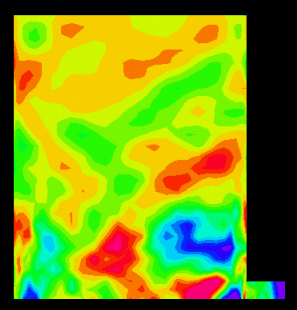
図2、Newmark法、減衰無し(δ = 0.5, α = 0.25) 
図3、Newmark法、レイリー減衰、C=0.001K 
図4、Newmark法、数値減衰 (δ = 0.6, α = 0.3025) 
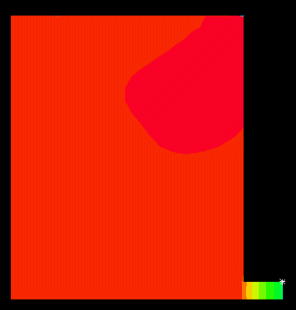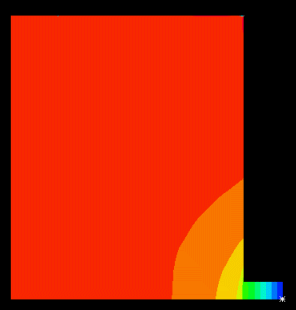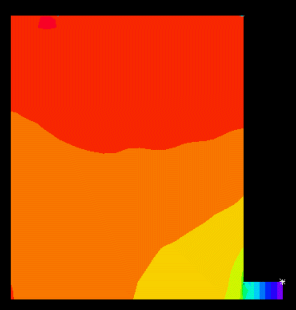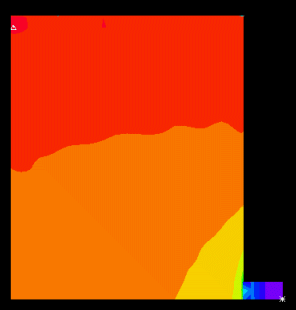
図5、Bathe法、物理減衰無し 上記ケースの研究を考察すると、物理減衰または数値減衰の存在が、全振動を抑制する ようにNewmark法を使った結果を改良している一方で、減衰は高レベルまで増やさねば ならないということが分かります。これは望ましくはありません。 しかしながら、Bathe法を使うと、著しい改善が見られます。 注目する点は、このケースは、数値パラメータ調整が必要無い事です。 そして、モデル内に人工的な物理減衰モデルが含まれていない事です。 従って、Bathe法は、大変形での長時間持続問題に適していると記述され、また、これら非線形FSI問題 でもとても魅力的です。 接触のがたつきは、通常のNewmark法や他の解法で使う数値減衰パラメータによって、大きな誤りの原 因になるかもしれません。 (参考文献[2]を参照下さい) 上記解析はシンプルな問題に着目していますが、上記の現象はかなり一般的で、大規模 な実際問題で起きます。 Onsala Ingenjorsbyra社の条件により、データの財産的価値で、私達は実際の原子炉数個の内の一部しか 示していません。 結果は、Onsala Ingenjorsbyra社が研究したもので、私達のTech Briefに掲載するため、快くデータ提供さ れたものです。 

図6 実際の原子炉の有限要素モデルと内部構成 最終的に、Bathe法は、解析時間を約50%多く使いますが、もし同じタイムステップがNewmark法で使わ れた場合、明らかに、解析の安定性と精度は、追加された解析コストを上回ります。 また、多くの解析において、Bathe法は明らかに大きな時間ステップを使うことができ ます。 類似したADINAの適用事例は、このNuclear Industryページを参照下さい。 参考文献 1. K. J. Bathe, Finite Element Procedures, Prentice Hall, 1996. 2. K. J. Bathe, "Conserving energy and momentum in nonlinear dynamics: A simple implicit time integration scheme", Computers and Structures 85:437-445, 2007. キーワード: 陰的時間積分、Newmark, Bathe時間積分、step by step時間積分、加速度、安定性、 2次精度近似、接触がたつき、流体構造相互作用、非線形動的、台形則
|