|
The Periodic Boundary Condition in ADINA CFD ADINA-CFDにおける、周期境界条件 このニュースでは、ADINA-CFDの周期境界条件のオプションについて説明します。 これらの境界条件は、流体内の流れと物理形状が周期的な場合に有効です。 この機能について、2つの例題を提示します。 最初の例題は、図1の2次元の翼列の間を通る流れです。 この解析は、シンプルですが説明に役立ちます。
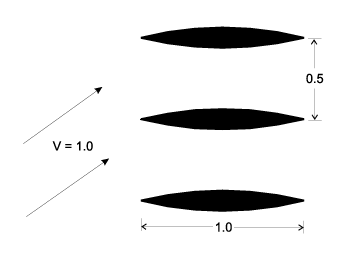
図1:2次元の翼列の間を通る流れ:概略図
流体形状が対称により、1つの流路と周期境界条件で計算可能です。
図2に使用したメッシュを示します。
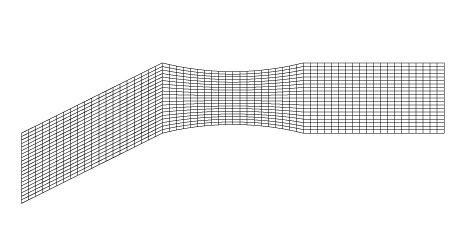
図2:2次元の翼列の間を通る流れ:メッシュ
図3,4では解析結果を示します。
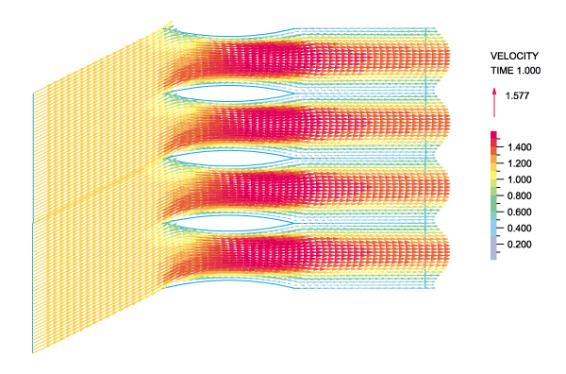
図3:2次元の翼列の間を通る流れ:流速ベクトル図
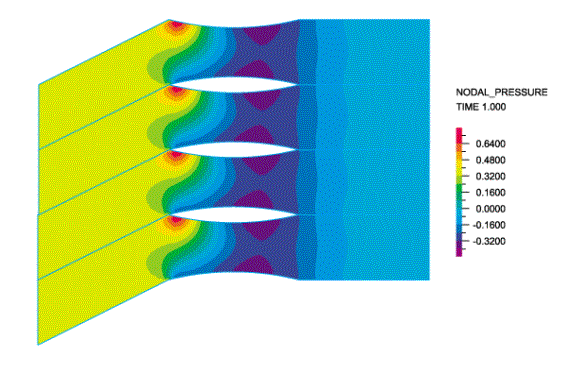
図4:2次元の翼列の間を通る流れ:圧力コンター図
2つ目の例題は、図5のパイプ内のプロペラ駆動による流れを示します。
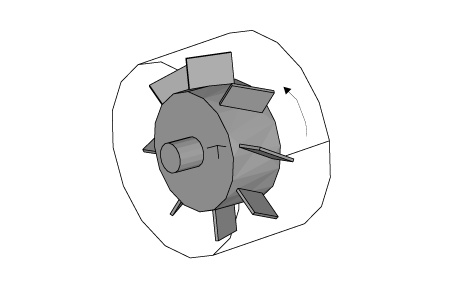
図5:パイプ内の回転プロペラ:概略図
1つのセンタードラム上に、プロペラセットが、周期対称に8枚の翼で構成されます。
周期境界条件を適用し、計算パフォーマンスにおける領域を局部的に小さくモデル化できます。
図6,7にこれを示します。

図6:計算領域の周期境界条件(表示:EnSight使用)
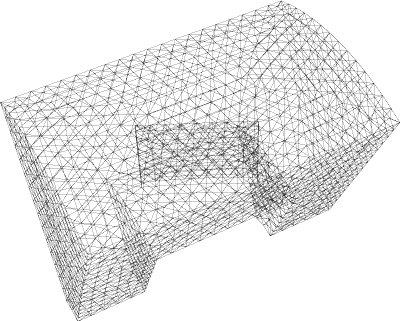
図7:計算領域のメッシュ(表示:EnSight使用)
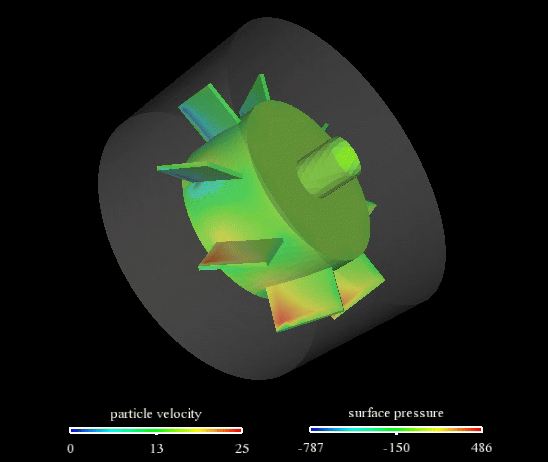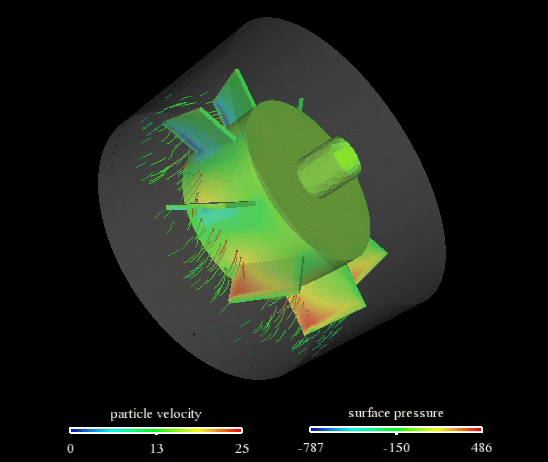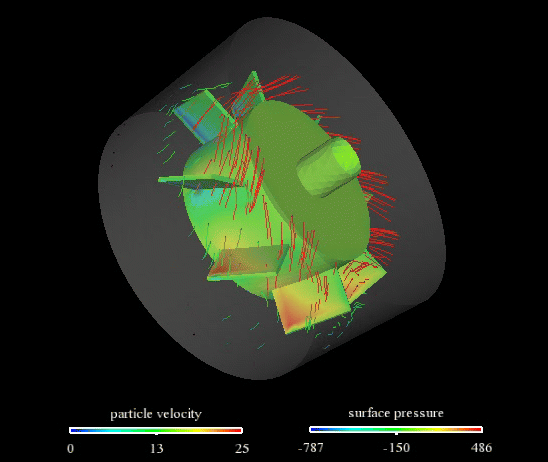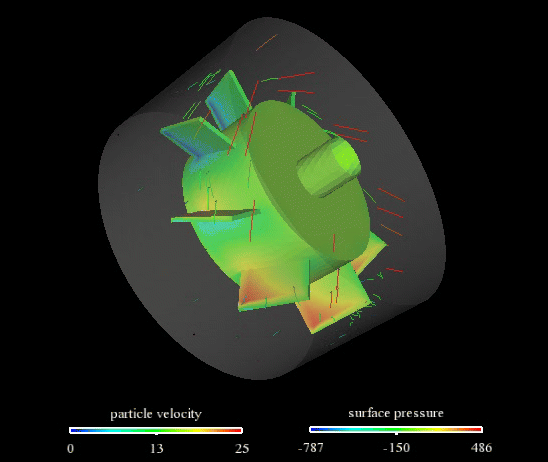
ページトップの動画は、流速と圧力結果です。
図8は、周期対称条件を用いた、1周期分の圧力結果です。
図9は、全体形状をモデル化した圧力結果です。
結果は同じですが、周期対称条件のほうが、全体形状に比べ、短時間の保存と少ないメモリで計算
できます。
また、周期境界条件により、境界面上のメッシュパターンを一致する必要が無いのがポイントです。
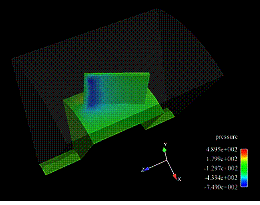
図8 ブレード周りの圧力、1周期分、(表示:EnSight使用)

図9:ブレード周りの圧力、全体形状、(表示:EnSight使用)
ADINAのCFD計算において、周期対称条件が可能になったことは、周期流れ解析において、便利で効
率的です。
解析者の少ない手間、少ない解析時間とメモりで、正確な結果を得ることができます。
実際にこのオプションは、妥当なコストで、多くの形状の複雑な3次元流体を解析するのに非常に重
要です。
キーワード
周期対称、サブ構造、周期的、境界条件、対称流れ、FCBI、CFD、プロペラ、駆動流、ポンプ
|