Noh-Bathe法による陽的時間積分法
2013.11.15 The Noh-Bathe Explicit Time Integration Method
陽的時間積分は、波動伝播問題を解析するのに幅広く利用されています。 陽的時間積分でよく使われるスキームは、中央差分法です。 しかしながら、このスキームは2つの制約があります。
1つ目の制約。中央差分法により得られる予測応答が、高周波において誤振動となります。 これらは、選ばれたメッシュでは表現できない、固有値とモードです。 理想的には、これらモードはどの応答においても、自動的に抑制されることです。 (しかも精度を落とさずに、メッシュによる表現できる固有値とモードで。)
2つ目の制約。中央差分法を使用したときの減衰の導入(誤振動を抑制するまたは静的解を得るた めの)は、計算の有効性を保持するために指定された、対角の減衰マトリクスのみです。[参考文献1] これは、ADINAを使う場合も同じです。
新しい陽的時間積分スキーム[参考文献2]は、ADINA9.0で実装されます。Noh-Bathe法になります。 このスキームは、いかなるパラメータを使わずに、高周波の応答を自動的に抑制します。 (空間分解するモードを正確に積分します。)このスキームはまた、非対角減衰マトリクスを使います。 減衰マトリクス無しでの、同じメッシュにおける計算に使われるコストは、中央差分法を使うコストより 少し大きいだけです。 このショーケースでは、以下事例による、Noh-Bathe法による陽的時間積分法の有効性を紹介します
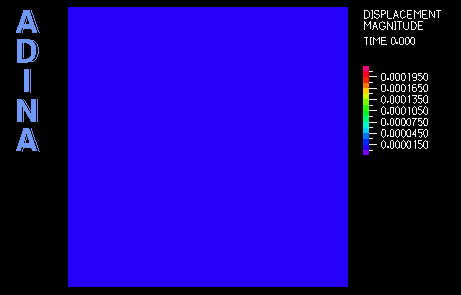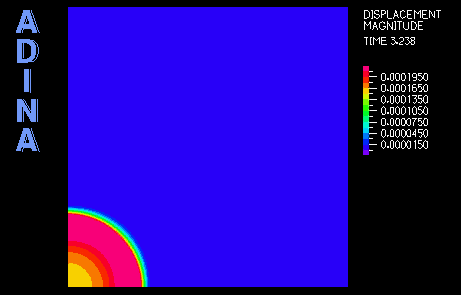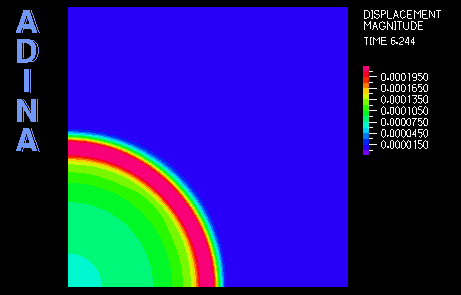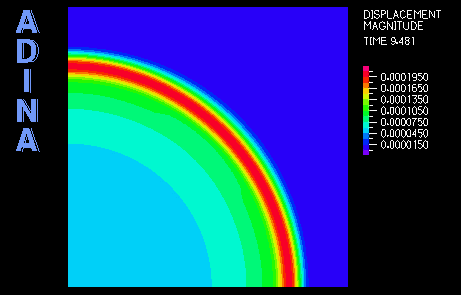
最初の事例は、単純波動伝播問題の解析です。(参考文献2からも参照できます。) 図1は、問題の概略図です。図2は計算された応答図です。
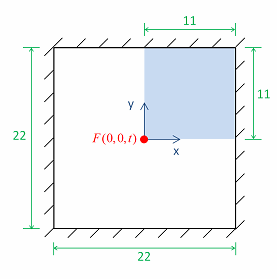
これにより、88×88のMITC4シェル要素を使った1/4対称モデルにします。
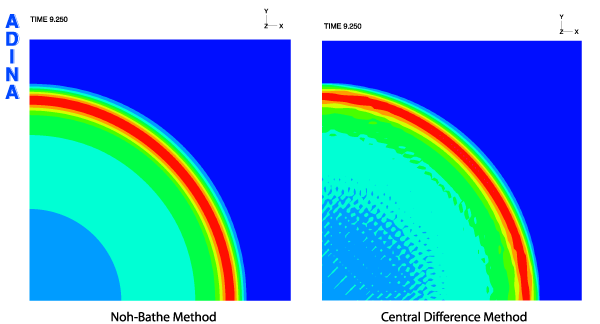
この比較で明白に、Noh-Bathe法のほうが、波動伝播応答解析で効果的であることがわかります。 詳細とこの例題の応答計算については、参考文献2を参照ください。
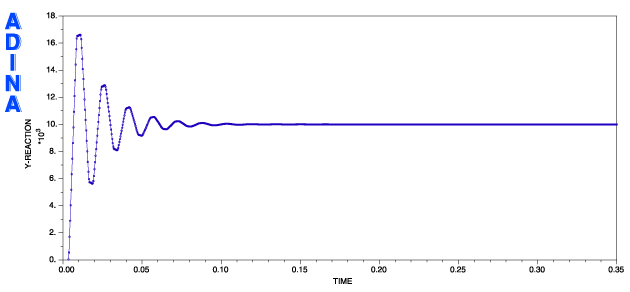
2つ目の事例は非対角減衰マトリクスを使用し、陽的時間積分で静的応答を得ることを説明します。 とても大規模な有限要素モデルを解く必要があって剛性マトリクスの分解に計算コストを要するような時、 あるいは、マトリクスがかなり悪い状態にある時、静的応答に対するこのアプローチは役に立ちます。 この簡易事例解析では、ロッド上の反力が予測されます。 20本のトラス要素でモデル化したロッドは片側拘束され、もう片側に圧縮荷重が負荷されます。 静的な解を得るためにレイリー減衰を導入します。
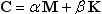
Noh-Bathe methodを使うことで荷重を急に与えることができ、かつ、300ステップだけで静的応答が得られます。 図3は固定端における反力に対して得られた結果になります。
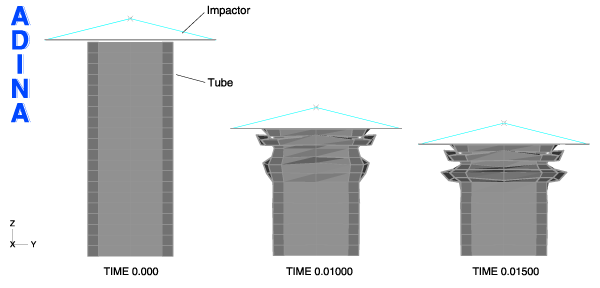
3番目の事例は、チューブの圧壊テストの解析です。 エンジニアはテスト中の衝撃装置の加速度レベルに興味を持ちます。 図4は3つの異なる時間での変形図です。図5は加速度-時間でのグラフです。 グラフで再認識できるのは、中央差分法解析では誤振動が見られますが、Noh-Bathe法では そのような振動はありません。
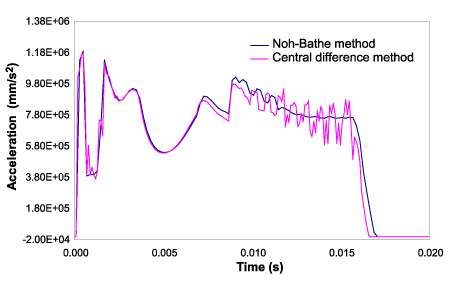
これらの解析事例等は、陽的時間積分でNoh-Bathe法を使ったメリットがしめされています。 Noh-Bathe法では、解析で誤った高周波振動は発生しません。そして、非対角項(レイリー減衰のような) が含まれます。これは、ADINAが広範囲の解析問題に有効となる、刺激的な開発です。
参考文献
[1] K.J. Bathe, Finite Element Procedures, Cambridge, MA: Klaus-Jurgen Bathe, 2006.
[2] G. Noh and K.J. Bathe, "An Explicit Time Integration Scheme for the Analysis of Wave Propagations", Computers & Structures, 129:178-193, 2013.
キーワード
陽的時間積分法、中央差分法、誤振動、chattering、Noh-Bathe法、レイリー減衰、非対角減衰マトリクス
