Mechanics of Thin-walled Open-section Beams

開口断面薄肉梁のメカニズム

薄肉梁のメカニズムは長い間、研究が続いています。しかし、たいていの実務者の発想は線形微小変

形に基づいており、変形モード(軸方向、曲げ方向、捩り方向、反り方向)の連成（Coupling）は考慮して

いません。(非連成の仮定)

しかしながら、3次元のビーム要素問題において、非連成の仮定は微小変形で、断面形状が2軸対

称（上下左右対称）のものに対してしか有効ではありません。大変形の場合たとえビーム要素の断面

形状が2軸対称でも異なったモードの連成が生じるため、非連成の仮定は崩れます。

正確にこれらの連成効果を考慮するためには、断面のゆがみ（いわゆるワグナー効果）や梁断面重心点の

せん断中心の偏心等、多くの現象を考える必要があります。

ADINA8.7において、すべての連成効果を考慮した、新しいビーム要素（ワーピングビーム要素）が導入

されました。このワーピングビーム要素は、ワーピング（反り）の自由度（注1）も含まれます。

（注１：ADINA8.7新設自由度）そしてまた、ワグナー効果と呼ばれる大きいねじれにより起こる、軸方向

のひずみも含みます。

過去のニュースで、横座屈でワーピングビーム定式化の結果と、1軸対称I型断面のビーム要素の線

形化座屈解析結果を示しました。今回のニュースでは、新しいワーピングビーム要素を使った、薄肉開

口断面梁（開いた断面の薄肉梁）で解析したメカニクスの事例をいくつか紹介します。各例題毎に、ワーピン

グビーム要素を用いた解析結果はMITC4シェル要素と比較されています。目的は、薄肉開口断面梁の

挙動を示しワーピングビーム要素の精度を評価することです。

始めに、チャネル断面（図1参照）の片もち梁の線形振動をとりあげモードと固有値を求めます。

梁の端面は全変位、全回転とワーピング自由度が拘束されています。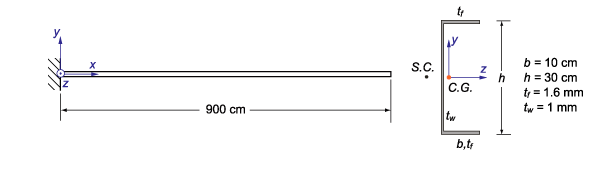

図1 溝型断面の片持ち梁の自由振動

まず、下のアニメーションは、梁の第1第2モードです。

ぱっと見たとき　モードが、断面の2本の主要な軸方向の曲がりのみ表していると思いがちです。

さらには、最も低いモードでは強度の弱いY軸まわり方向曲がるはずであり、そして、モード数が増すに

従い、強度の強いZ軸まわり方向に曲がるはずだと思うに違いありません。

ところが、1モード目の弱い軸については純曲げ方向になりますが、2モード目は純曲げ方向ではなく、

代わりに、軸方向に曲がりとねじれが同時に起きています。

これは、曲げと捩りの連成において、重心点のせん断中心の偏心が起こるためです。

表1はシェル要素モデルとワーピングビーム要素モデルの固有値比較で、新しいワーピングビーム要素

モデルの精度はかなり良好なことがわかります。

１次モード

2次モード

表1溝型断面のワーピングビーム要素とシェル要素の固有値結果比較

モード

予測とおり、梁の固有値は、シェル要素よりも、わずかに高く硬く出ています。大変形

の仮定により梁がわずか硬くなっているからです。

「2次モードでは曲がりとねじれは連成されますが、なぜ1次モードでは連成されないのか」という疑問

が出てくるでしょう。

その理由は、ビームが　x-z面で対称な面で曲がるとき、対称性が捩れを阻止するのです。

しかしながら、対称面外に曲がった場合は、応答は同時に曲げと捩れは連成され、ねじれは純曲げと比

べて、小さいひずみエネルギーを求めます。

続いて、図2にあるような十字型の2軸対称断面について考えます。

この問題によって、軸力と捩りの連成が非常に重要であることがわかります。

軸力を求めるX並進自由度以外の梁両端面の全並進変位と回転とワーピング自由度を拘束します。

MITC4シェル要素を用いた梁とワーピングビーム要素を用いた梁に対しての線形化座屈解析を行います。

下のアニメーションによって、MITC4シェル要素を使った、最小の座屈モード、2番目の座屈モード、

３番目の座屈モードがわかります。

座屈モードを良く見ると、断面が中心線周りに捩れても、断面の中心線は常に直線（つまり曲がらない）

であることに注意ください。

表2は、ワーピングビーム要素モデルで計算した座屈荷重結果と理論解（閉形式解）との比較です。

「参考文献1,2参照」

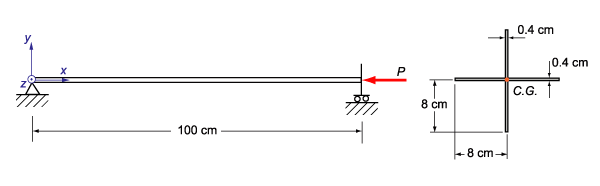
図2 十字型断面梁の線形化座屈解析

1次モード

2次モード

3次モード

表2　ワーピングビーム要素で計算した線形化座屈荷重と理論解（閉形式解）

2軸対称断面で、梁の長さが短い場合、この座屈モード（軸-ねじれ）が卓越します。

しかしながら、梁の長さが長い場合は、オイラー座屈モードが卓越します。

続いて、図3にあるような1軸対称のI型断面梁の線形化座屈解析について考えます。

軸力を負荷するZ並進自由度を除いた、全並進自由度は拘束されます。

回転については、両端のZ軸周りのみ拘束されます。ワーピング自由度は両端でフリーです。

下のアニメーションで、この断面の第一座屈モードが見られます。

この事例では　軸力-屈曲-ねじりの連成の効果が良く現れています。ワーピングビーム要素モデルを

使った座屈荷重は、閉形式解で表された理論解に極めてよく一致します。（参考文献1参照）

ご覧頂けるように、座屈モードは捩れとY-Z対称面外方向の曲げが複合しています。

これは、1軸対称断面の応答の特徴です。

断面の非対称性により、捩れの増加と対称面外方向曲げとの連成の自由度がより顕著になります。

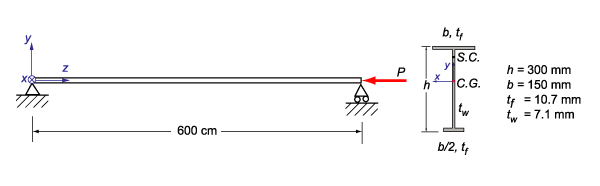
図3 1軸対称I型断面の線形化座屈解析

次の事例は、再びチャネル断面について考慮した事例（図4）になりますが、大変形解析を用います。

集中荷重を断面の重心点に負荷し、Y方向に負荷したケースと、Z方向に負荷したケース

の2ケースで解析します。片側の端面をクランプ（完全拘束）されています。ワーピン

グ自由度も拘束されます。

図5,6は、ワーピングビーム要素とMITC4シェル要素を用いたY方向荷重時の荷重-変位

曲線です。両者の解は極めてよく一致しています。

このページ冒頭にあるアニメーションは、Y方向負荷時の変形図です。

その下にあるアニメーションがZ方向負荷時の変形図になります。

ご覧頂けるように、Y方向負荷時、初めのうちは、Y方向に梁は動き、Z方向の変形とね

じれはほとんどありません。しかし、ある臨界値を超えると、断面はかなりねじれ始

めて、梁のZ方向の動きは著しくなります。

しかしながら、Z方向の荷重負荷した場合、梁は捩れを伴わないでX-Z対称面内曲がり

ます。

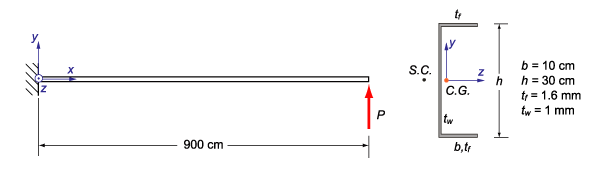
図4　チャンネル断面の片持ち梁の大変形解析

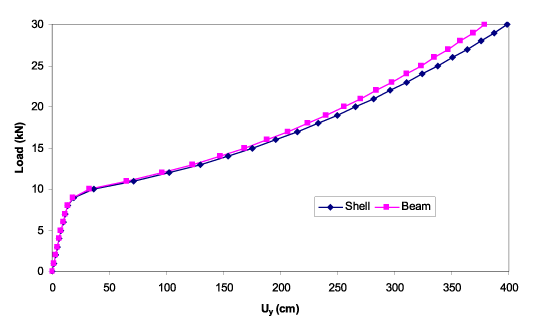
図5　チャンネル断面の梁先端荷重とY方向変位グラフ（Y方向負荷時）

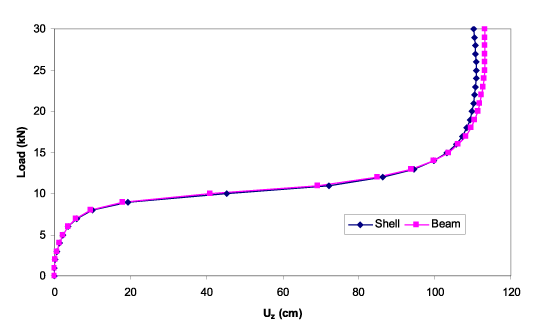
図6　チャンネル断面の梁先端荷重とZ方向変位グラフ（Y方向負荷時）

ビームの大変形問題では　せん断中心の重心に対する偏心が無視できないことがこの事

例から良くわかります。

開口薄肉断面梁が大きく捩れた場合、「曲げ」と「捩り」と「ワーピング」の連成お

よび、ワグナー効果が無視できないこともわかります。

最後の事例では、同じチャネル断面の応答を検討しますが、今回は自由端に、トルク荷重

を負荷します。つまり重心に負荷されたわけです。（図7参照）

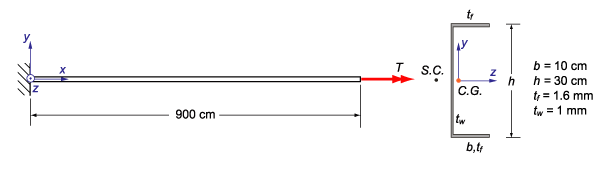
図7　捩れによる、溝型断面の大変形解析

端面の全並進自由度と回転自由度とワーピング自由度は拘束されています。ぱっと見た

とき、工学的な直感では、断面が中心線に関して、ねじれるだけと思いがちです。

そして、ビームは曲がらないと思うでしょう。

しかしながら、実際は下のアニメーションにご覧頂けるとおり、この1軸対称断面によ

る曲げと捩りの連成で、ねじれは初め、y方向の変形だけですが、より大きくねじれると、

Z方向にも変形します。

ワーピングビーム要素やMITC4シェル要素を用いると梁の先端のY方向変位がトルク

の関数になっていることが図8からわかります。ワーピングビーム要素とMITC4シェル

要素の解は極めてよく一致しています。

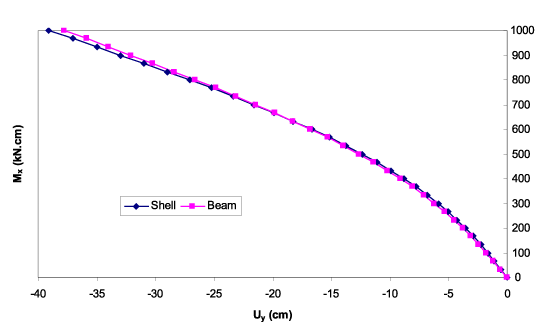
図8　チャンネル断面先端の捩りモーメントとY方向変位

スレンダー構造物の場合、厳密な定式化に基づいたビーム要素を用いれば、3Dシェル要

素と同等な結果を得ることができ、計算コストを下げられることがこれらの事例から

わかります。

ただし仮定される大変形には　前述の連成現象を十分に考慮されていなければなりま

せん。シェル要素モデルと比べると、ADINAの新しいワーピングビーム要素を用いると、

計算コストはもちろんのことモデル作成時間と結果評価時間も非常に短縮できます。

[参照文献]

1.      S.P. Timoshenko, J.M. Gere, Theory of Elastic Stability, McGraw-Hill, 2^nd edition,

 1961

2.      Z.P. Bazant, L. Cedolin, Stability of Structures: Elastic, Inelastic, Fracture and

 Damage Theories, Oxford University Press, 1991

今回のような梁の挙動と様々な定式化の更なる研究について、以下の参考書、論文をご

参照ください。似たような例が取り上げられています。

* H. Wagner,“Torsion and buckling of open sections”, 

Technical Memorandum No. 807, 1936, National Advisory Committee for

 Aeronautics (This is THE classical work!)

* A. Conci,“Large displacement analysis of thin-walled beams with 

generic open sections”, International Journal for Numerical Methods in

 Engineering, 33, 1992, pp. 2109-2127

    * N. S. Trahair, Flexural-Torsional Buckling of Structures, CRC Press, 1993

* B. A. Izzuddin, D. Lloyd Smith, “Large displacement analysis of

 elastoplastic thin-walled frames. II: verification and application”,

 Journal of Structural Engineering, 12, 1996, pp. 915-925

* F. Gruttmann, R. Sauer, W. Wagner, “A Geometrical Nonlinear Eccentric 

3D-Beam Element with Arbitrary Cross-Sections”, Computer Methods in 

Applied Mechanics and Engineering, 160, 1998, pp. 383-400.

* K. M. Hsiao, W. Y. Lin, “A co-rotational formulation for thin-walled 

beams with monosymmetric open sections”, Computer Methods in Applied

 Mechanics and Engineering, 19, 2000, pp. 1163-1185

* M. Y. Kim, S. P. Chang, S. B. Kim, “ Spatial postbuckling analysis of

nonsymmetric thin-walled frames. II: geometrically nonlinear finite 

element procedures”, Journal of Engineering Mechanics, 127, 2001, 

pp. 779-790

* Y.-L. Pi, M. A. Bradford, “Effects of approximations in analysis of beams

 of open thin-walled cross-section-part I: Flexural-torsional stability”,

 International Journal for Numerical Methods in Engineering, 51, 2001, pp.

 757-772

* J. M. Battini, C. Pacoste, “Co-rotational beam elements with warping

 effects in instability problems“, 

Computer Methods in Applied Mechanics and Engineering, 191, 2002, pp. 

1755-1789

* F. Mohri, N. Damil, M. P. Ferry, “Large torsion finite element model 

for thin-walled beam”, Computers and Structures, 86, 2008, pp. 671-683 

キーワード：

薄肉開口断面、ワーピング、反り、大変形、ワグナー効果、軸捩り座屈、横座屈、

MITC4シェル、大捩れ、線形化座屈、ポスト座屈、曲げ-ねじり連成、軸-ねじり連成、

軸-曲げ-ねじり連成